Cyclic symmetries
This article deals with the four infinite series of point groups in three dimensions (n≥1) with n-fold rotational symmetry about one axis (rotation by an angle of 360°/n does not change the object), and no other rotational symmetry (n=1 covers the cases of no rotational symmetry at all):
Chiral:
- Cn (nn) of order n - n-fold rotational symmetry (abstract group Cn); for n=1: no symmetry (trivial group)
Achiral:
- Cnh (n*) of order 2n - prismatic symmetry (abstract group Cn × C2); for n=1 this is denoted by Cs (1*) and called reflection symmetry, also bilateral symmetry.
- Cnv (*nn) of order 2n - pyramidal symmetry (abstract group Dn); in biology C2v is called biradial symmetry. For n=1 we have again Cs (1*).
- S2n (n×) of order 2n (not to be confused with symmetric groups, for which the same notation is used; abstract group C2n); for n=1 we have S2 (1×), also denoted by Ci; this is inversion symmetry
They are the finite symmetry groups on a cone. For n = 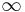 they correspond to four frieze groups. Schönflies notation is used, and, in parentheses, orbifold notation. The terms horizontal (h) and vertical (v) are used with respect to a vertical axis of rotation.
they correspond to four frieze groups. Schönflies notation is used, and, in parentheses, orbifold notation. The terms horizontal (h) and vertical (v) are used with respect to a vertical axis of rotation.
Cnh (n*) has reflection symmetry with respect to a plane perpendicular to the n-fold rotation axis.
Cnv (*nn) has vertical mirror planes. This is the symmetry group for a regular n-sided pyramid.
S2n (n×) has a 2n-fold rotoreflection axis, also called 2n-fold improper rotation axis, i.e., the symmetry group contains a combination of a reflection in the horizontal plane and a rotation by an angle 180°/n. Thus, like Dnd, it contains a number of improper rotations without containing the corresponding rotations.
C2h (2*) and C2v (*22) of order 4 are two of the three 3D symmetry group types with the Klein four-group as abstract group. C2v applies e.g. for a rectangular tile with its top side different from its bottom side.
Examples
| S2/Ci (1x): | C4v (*44): | C5v (*55): | |
|---|---|---|---|
Parallelepiped |
Square pyramid |
Elongated square pyramid |
Pentagonal pyramid |